Enhanced operation of PVWPS based on advanced soft computing optimization techniques

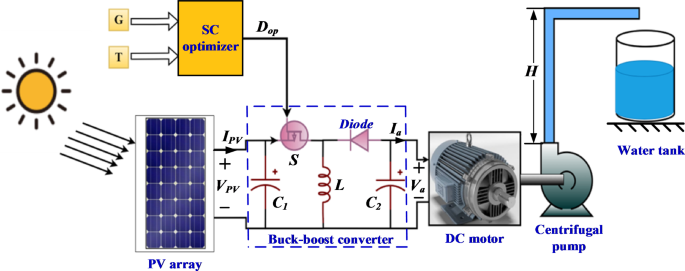
Tender computing (SC) optimizers are used to maximise the output energy of the photovoltaic panels. They supply accuracy and pace in acquiring the optimum obligation cycle (D_op) contemplating surprising modifications and disturbances occurring in numerous environmental situations. By adjusting each present and voltage of the photovoltaic panels, the optimum obligation cycle D_op is achieved, considering the continual monitoring of the ambient temperatures and the photo voltaic radiation affecting the PV module. Three smooth computing optimization algorithms are used to attain the D_op that are: Honey Badger Algorithm (HBA), Snake Optimization Algorithm (SOA), and Gorilla Troop Optimization Algorithm (GTO). The required goal to be achieved by making use of these SC algorithms is to acquire the optimum obligation cycle (D_op) that achieves a world most energy level for the photovoltaic module (P_PV) and decrease the losses of the DC motor (P_loss). Consequently, the motor effectivity (η) will likely be improved and the water movement charge of the motor-pump set (Q) is maximized. The required goal capabilities used within the proposed algorithms will be represented mathematically as in (8). The proposed optimizers are expressed within the block diagram proven in Fig. 5.

Block diagram of the proposed SC optimizers for PVWPS.

DC motor constraints

To make sure that the DC motor works safely, a number of constraints associated to the utmost energy management system have to be taken under consideration. These constraints are divided into two primary sorts: equality or inequality constraints. The imposed situations have to be totally glad in case of equality constraints, whereas in inequality constraints, the imposed situations will be partially fulfilled, considering the permissible tolerances that don’t disturb the protection of the system. The implementation of those constraints is an pressing want to make sure that the DC motor operates inside the security limits and with excessive reliability, considering the undesirable environmental modifications. The constraints at which the DC motor should function will be expressed as in (9) and (10).

Gorilla troop algorithm

It’s a sort of metaheuristic optimization algorithm. This kind of algorithm was created by monitoring the social habits of gorilla troops. A simulation of the habits of teams of gorillas was carried out to search out the optimum answer by sharing data and bettering their motion and decision-making⁴⁰. The gorilla troop (GTO) algorithm makes use of the habits of gorillas led by a silverback as inspiration for its reconnoitering stage. Gorilla and silverback symbolize the options nominated by the algorithm, and it was indicated that silverback is the popular answer between them.

The algorithm makes use of three mechanisms to traverse the issue area, the primary is migration to unknown areas, via which the entire downside area is explored, the second is migration to identified areas, via which exploration effectivity will be enhanced, whereas the final is named relocating to a different gorillas, which aids to avert native optimum factors. These mechanisms depend upon the coefficient “p” and are modeled utilizing an equation to facilitate reconnaissance. Equations (11) and (12) had been used to simulate the three mechanisms concerned within the reconnoitering stage. All particulars and symbols are outlined in⁴¹.

the place

Within the exploitation stage of gorilla troop algorithm, two strategies are adopted, impressed by the habits of gorillas, one in every of which is “Observe the silverback” and the opposite is “Competitors for grownup females”. Within the first methodology situation, the silverback is chargeable for main the group and making choices. When the silverback turns into weak or dies, competitors happens between different males to achieve the management of the group, along with the collection of grownup females. The selection between the 2 strategies relies on the worth of C talked about in (12). When C ≥ W, the mechanism “Observe the silverback” is chosen, however when C W, the “Competitors methodology for grownup females” is essentially the most appropriate for choice. W is a coefficient positioned earlier than the optimization course of. A simulation of the observe silverback is made to indicate its habits utilizing the Eq. (13), whereas the habits of a contest mechanism for grownup females is proven via the Eqs. (14) and (15). A abstract of the steps describing the gorilla troop (GTO) algorithm is current as illustrated in Fig. 6.

Flowchart for the gorilla troop optimization algorithm.

Honey badger algorithm

The honey badger is without doubt one of the mammals identified for its braveness that takes semi-deserts and African rainforests as a refuge to dwell in. From the successive follow-up of those mammals whereas looking for meals, a easy optimization mechanism referred to as the honey badger algorithm (HBA) was found. The honey badgers can acquire foraging in one in every of two methods, both by finding the prey utilizing its robust sense of odor, or by digging to achieve the meals. As well as, the areas of the beehives will be identified by monitoring the honey information birds. These two strategies had been known as the “digging stage” and the “honey stage”, respectively. The honey badgers can transfer rapidly or slowly primarily based on the power of the scent of the prey. In case of robust scents, its pace could be very excessive and vice versa. The fundamental management procedures and equations of the honey badger algorithm (HBA) will be summarized as follows⁴²:

1. (a)

   Initialization stage of the HBA: The quantity (N) and areas of honey badgers are initialized in response to Eq. (16).

   $${x}_{i} = {lb}_{i} + {r}_{1} occasions left({ub}_{i} – {lb}_{i}proper)$$

   (16)

   the place r₁ is a random worth starting from 0 to 1, the decrease and higher bounds are expressed in lb_i and ub_i, respectively, and x_i is ith location of the honey badger that gives a candidate answer in its inhabitants group N. honey badger place referring to a candidate answer in a inhabitants of N, whereas and are respectively decrease and higher bounds of the search area.

2. (b)

   Decide the depth (I_i): The depth of the prey scent (I_i) is determined by the situation of the ith honey badger, the farther the honey badger is from its prey, the much less intense it’s and vice versa. If the depth of the odor is excessive, the honey badger will transfer in a short time, and the decrease the depth, the slower the pace. The connection between distance and depth will be represented by making use of the inverse sq. legislation as in (17).

   $$left{start{array}{c}{I}_{i}={r}_{2}occasions frac{S}{{4pi d}_{i}^{2}} S={left({x}_{i}-{x}_{i+1}proper)}^{2} {d}_{i}={x}_{prey}-{x}_{i}finish{array}proper.$$

   (17)

   the place r₂ is a random worth starting from 0 to 1, S is the focus depth which displays the situation of the prey (location of prey), x_prey is the situation of the prey (finest location), and d_i is the separation between the ith badger and its prey.

3. (c)

   Replace density issue (α): To attain a clean transition from the exploration stage to the exploitation stage, the random distribution that modifications with time is managed by the density issue (reducing issue) (α). α is up to date by utilizing the mathematical Eq. (17) that ensures a gradual lower with every iteration and subsequently the extent of randomness will be diminished over time.

   $$alpha =Ctimes {e}^{left(frac{-t}{{t}_{max}}proper)}$$

   (18)

   the place t_max is the utmost variety of iterations, and C is a continuing bigger than 1.

4. (d)

   Escaping from native optimum: This process and the following two are used to stop being caught in native optima areas. This algorithm provides a flag F that modifies the search path, offering brokers extra alternatives to correctly discover the search area.

5. (e)

   Updating the positions of brokers: The “digging stage” and the “honey stage” are two indifferent steps that kind the place updating course of (x_new) for HBA. These phases have varied capabilities, that are described in particulars beneath:

   • Digging stage: The motion sample of the honey badger and the cardioid kind are very related; as well as, the cardioid movement will be simulated by the connection described in (19). Throughout this stage, the honey badger particularly makes choices primarily based on this equation.

     $${x}_{new}= {x}_{prey} + F beta {I}_{i} {x}_{prey} + left(F {r}_{3} alpha {d}_{i}occasions left|mathit{cos}left(2pi {r}_{4}proper)occasions left[1 -mathit{cos}left(2pi {r}_{5}right)right]proper|proper)$$

     (19)

     the place β (≥ 1) is the aptitude of the honey badger to acquire meals, and r₃, r₄, r₅, r₆, and r₇ are random values starting from 0 to1.

The flag F modifications the path of the search and will be calculated as in (20):

The honey badger exploits distance data (d_i) to information its search when it’s close to its prey location (x_prey). Furthermore, its habits is affected by the time-varying looking out sample (α), nevertheless it may possibly encounter disturbances F whereas looking out. A abstract of the steps describing the honey badger algorithm (HBA) is introduced as depicted in Fig. 7.

Flowchart for the honey badger optimization algorithm.

Snake algorithm

It’s an optimization algorithm found in 2019. It mimics the exercise and motion of a snake within the nature. When making use of this algorithm, essentially the most appropriate snakes are chosen to function dad and mom for the following era, after a re-evaluation of the health of every snake individually throughout motion. After that, the dad and mom are uncovered to numerous genetic modifications represented in crossover and mutation, which permits the manufacturing of a brand new group of snakes. The fundamental steps and equations of the snake algorithm is introduced as follows⁴³:

1. (a)

   Initialization: a random inhabitants with a consolidated distribution is generated. The Eq. (22) gives the preliminary inhabitants.

   $${X}_{i} = {X}_{min} + r left({X}_{max}- {X}_{min}proper)$$

   (22)

   the place X_i is the situation of ith people, r is a random worth starting from 0 to 1, and X_max, X_min are the higher and decrease bounds respectively. The inhabitants is represented by each men and women, the place every sort constitutes half (50%) of the inhabitants.

2. (b)

   Defining Temperature and Meals Amount: The meals high quality (Q) together with the temperature (Temp) will be decided by Eq. (23), whether it is attainable to find out upfront the most effective male, the most effective meals location, the most effective feminine and the most effective particular person in every group.

   $$left{start{array}{c}Temp={e}^{left(frac{-t}{T}proper)} Q={C}_{1}*{e}^{left(frac{t-T}{T}proper)}finish{array}proper.$$

   (23)

   the place t is the current iteration, T is the utmost variety of iterations, and C₁ is a continuing.

3. (c)

   Exploration stage (No Meals): When the worth of Q is lower than the minimal worth (0.25), the snakes start to seek for meals by selecting any random location after which replace their location accordingly. To simulate the exploration part, equation No. (24) will be adopted.

   $$left{start{array}{c}{X}_{i,m}left(t+1right)={X}_{rand,m}left(tright)pm {C}_{2} {A}_{m} left(rand left({X}_{max}-{X}_{min}proper)+{X}_{min}proper) {X}_{i,f}left(t+1right)={X}_{rand,f}left(tright)pm {C}_{2} {A}_{f} left(rand left({X}_{max}-{X}_{min}proper)+{X}_{min}proper)finish{array}proper.$$

   (24)

   the place X_i,m and X_i,f is the situation of the ith female and male particular person respectively, rand is a random worth starting from 0 to 1, A_m and A_f is the aptitude of the female and male to get the meals respectively, X_rand,m and X_rand,f is the situation of random female and male respectively.

4. (d)

   Exploitation stage (Meals Exists): If each the temperature (Temp) and meals high quality (Q) exceeded the edge (0.6) (scorching) and (0.25), respectively, the snake is not going to transfer besides within the case of meals solely. This motion will be expressed in Eq. (25).

   $${X}_{i,j}left(t + 1right)= {X}_{meals} pm C3 occasions Temp occasions rand occasions left({X}_{meals}- {X}_{i,j}left(tright)proper)$$

   (25)

The situation of a person male or feminine is represented by X_{i, j}, whereas X_meals signifies the situation of the most effective people. The snake mode will likely be decided in response to the edge worth. If the edge is lower than 0.6 (chilly), the snake can enter both combating mode or mating mode.

• Combating Mode: Every of men and women up to date its location in response to its combating functionality as introduced in (26).

  $$left{start{array}{l}{X}_{i,m}left(t + 1right)={X}_{i,m}left(t proper)pm {C}_{3} occasions FM occasions rand occasions left({X}_{finest,f}-{X}_{i,m}left(tright)proper) {X}_{i,f} left(t + 1right)= {X}_{i,f} left(t + 1right)pm {C}_{3} occasions FF occasions rand occasions left({X}_{finest,m} – {X}_{i,F} left(t + 1right)proper)finish{array}proper.$$

  (26)

  the place X_finest,f signifies the situation finest particular person of the feminine group, the male agent’s combating functionality is denoted by FM, whereas the situation of the most effective male particular person is denoted by X_{finest, m}, and the place of the ith feminine particular person is represented by X_i,f. FF stands for the feminine agent’s combating functionality.

• Mating Mode: Every of men and women up to date its location in response to its mating functionality as introduced in (27).

  $$left{start{array}{l}{X}_{i,m}left(t+1right)={X}_{i,m}left(tright)pm {C}_{3}occasions {M}_{m} occasions rand occasions (Q occasions {X}_{i,f}left(tright)-{X}_{i,m}left(tright)) { X}_{i,f}left(t+1right)={X}_{i,f}left(tright)pm {C}_{3}occasions {M}_{f} occasions rand occasions (Q occasions {X}_{i,m}left(tright)-{X}_{i,f}left(tright))finish{array}proper.$$

  (27)

  the place M_m & M_f refers back to the mating capacity of female and male respectively. Within the case of egg hatching, the worst female and male are chosen and changed as introduced in (28). A abstract of the steps describing the snake algorithm (SAO) is offered as depicted in Fig. 8.

  

  Flowchart for the snake optimization algorithm.

  $$left{start{array}{l}{X}_{worst,m}={X}_{min}+randtimes left({X}_{max}-{X}_{min}proper) {X}_{worst,f}={X}_{min}+randtimes left({X}_{max}-{X}_{min}proper)finish{array}proper.$$

  (28)

Neuro-fuzzy method

The adaptive neuro-fuzzy inference system (ANFIS) is a blended arithmetic mannequin that outcomes from integrating the adaptive studying talents of neural networks with fuzzy logic which might interpret and symbolize information. Sophisticated issues will be solved by neuro-fuzzy methods when neural community and fuzzy logic methods are mixed. ANFIS is characterised by its functionality of cope with linguistic and numerical expressions, moreover, the opportunity of coaching them via samples of enter–output knowledge. As well as, ANFIS could make correct choices, forecasts and enhance the efficiency of any system over time primarily based on its capacity to be taught from knowledge. It might replace and adapt its inside parts primarily based on examples of inputs and outputs via the coaching course of. Furthermore, ANFIS gives interpretability, robustness towards noise and uncertainty within the knowledge and transparency. Ambiguous or unsure information will be represented by fuzzy logic, inflicting the system to function with inaccurate knowledge. Incomplete and noisy data will be dealt with by producing a fuzzy logic mechanism that enhances the power of the system to cope with incomplete knowledge in the true world. However, sample recognition is completed with the opportunity of processing a considerable amount of large numerical knowledge via neural networks. Because of this, difficult real-world issues are successfully modeled and interpreted by adaptive neuro-fuzzy inference methods (ANFIS). In distinction to black-box fashions (deep neural networks), specialists can use fuzzy guidelines via ANFIS which can be straightforward to know and modify in order that these specialists can share their information and higher perceive the reasoning of the system²⁹.

Membership capabilities will be thought of as a necessary component of ANFIS, as a result of they play an important function in fuzzy inference. It allow the system to determine and manipulate linguistic variables, which results in straightforward decision-making and rule-based inference. As well as, it determines the diploma of membership and the credibility of the enter worth for a specific linguistic time period. It might additionally symbolize mysterious teams and outline their shapes and limits. The system can clarify and interpret unsure or inaccurate data by assigning membership levels. There are a number of types of membership capabilities, together with Gaussian, trapezoidal, and triangular, as well as they are often constructed by analyzing knowledge or figuring out the area. Applicable membership capabilities are chosen primarily based on a mixture of things together with knowledge evaluation, area information, and trade-offs between system efficiency and interpretability. To attain a particular neuro-fuzzy system, experimentation and iterative refinement have to be carried out to search out essentially the most acceptable membership capabilities. On this research a subclustering method was used to generate membership capabilities in ANFIS. This method breaks down the enter knowledge into small subsets to generate many native membership capabilities that choose up extra correct system traits. The development of adaptive neuro-fuzzy inference system is introduced as proven in Fig. 9.

Construction of ANFIS method.

Determine 10 presents the optimum obligation cycle (D_op) knowledge generated by the GTO optimizer alongside the outcomes from ANFIS, demonstrating the excessive accuracy achieved throughout the ANFIS coaching course of. As T rises, the D_op reveals a slight improve from roughly 0.25 to round 0.55. An analogous sample is noticed when G will increase from 0 to 1000 W/m², with obligation cycles steadily rising in each fashions. Each the GTO and ANFIS fashions seem to overlap considerably, indicating that each methods predict very related values for the D_op over the given vary of temperatures and irradiance. The proximity between the D_op of GTO and ANFIS suggests robust settlement between these fashions and the optimum values. The near-perfect overlap between GTO and ANFIS means that these strategies present extremely constant outcomes. The ANFIS mannequin appears to match carefully with the theoretical or optimized knowledge (D_op), which may point out a excessive predictive accuracy of the ANFIS system for this particular utility.

Comparability of D_op knowledge produced by the GTO optimizer and the outputs from ANFIS, considering T and G.