A general framework for active space embedding methods with applications in quantum computing

Any energetic area embedding strategy, the place a subset of electrons and orbitals of a system—the fragment—are embedded in an efficient potential generated by the remaining electrons of the programs and all of the ion cores—the atmosphere—could also be carried out within the common framework introduced on this work. Right here, we use the framework of multiconfigurational range-separated density practical principle (rsDFT)^{17,18,19,20,21,22,23,24} and the Gaussian and airplane waves (GPW) strategy²⁵, whereby the embedding potential is obtained from a mean-field methodology, whereas the fragment Hamiltonian is solved with a correlated wave perform ansatz. The strategy and infrastructure now we have developed are utterly common; it could actually deal with each molecular and periodic programs, it helps spin-polarized and unpolarized calculations, describes the core electrons explicitly or by pseudopotentials, and might be mixed with each classical WF and quantum circuit ansatzes alike.

Periodic energetic area embedding

To introduce the framework for AS embedding strategies, we begin with the second-quantized digital Hamiltonian within the Born-Oppenheimer approximation. This may be written in atomic models as

the place ({hat{V}}_{nn}) is the Coulomb repulsion between the nuclei, whereas h_pq and g_pqrs are one- and two-electron integrals given by

The variable x (({bf{x}}^{prime})) is a compound variable for the electron coordinates in area, r (({bf{r}}^{prime})), and its spin diploma of freedom. The operators (hat{h}) and (hat{g}) in Eqs. (2) and (3) account for the kinetic power of the electrons, the electron-nuclear attraction, and the electron-electron repulsion, and are outlined as

the place P labels the ion cores, whereas Z_P and R_P denote the corresponding nuclear costs and nuclear positions, respectively. The indices p, q, r, s label common one-particle features (spin-orbitals), whose corresponding sums showing in Eq. (1) run by your complete foundation set. The operator ({hat{a}}_{p}^{dagger }) (({hat{a}}_{p})) is a creation (annihilation) operator including (eradicating) an electron to (from) spin-orbital ψ_p(x). In an embedding strategy just like the one introduced right here, the fragment of curiosity is outlined when it comes to an energetic area consisting of a handful of energetic electrons and energetic orbitals. All of the electrons that aren’t a part of the AS sometimes occupy the low-energy states of the system and are referred to as inactive orbitals; see Fig. 1 for an instance of AS choice in molecules and supplies. As soon as the AS has been recognized, a corresponding embedded fragment Hamiltonian might be outlined in a fashion utterly analogous to Eq. (1), that’s

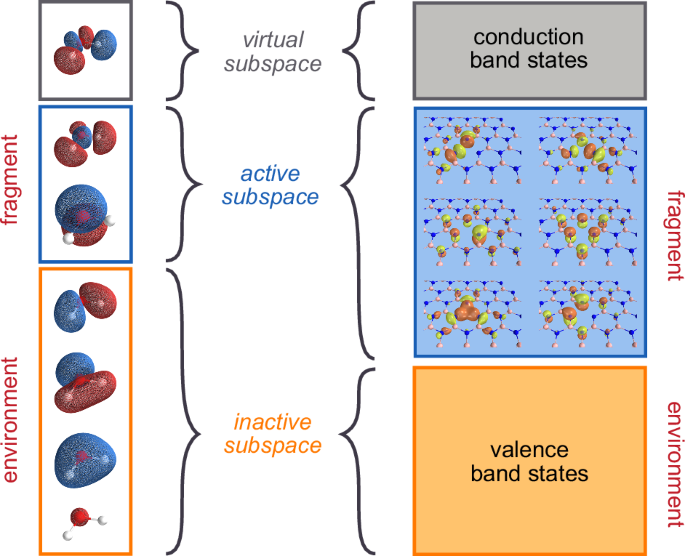
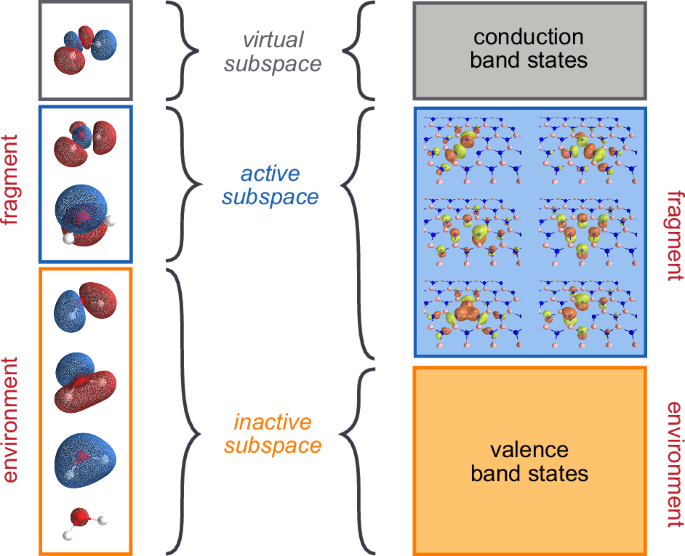
with the one distinction that the sums are restricted to the energetic orbitals, labeled by the indices u, v, x, y, and that the one-electron integrals, h_pq, have been changed by the weather of an embedding potential, ({V}_{uv}^{,textual content{emb},}). This potential accounts for the interactions between the inactive and energetic electrons along with the contributions from the one-electron integrals. Discover that till this level, this formulation is totally common; now we have not but specified learn how to compute the embedding potential. In precept, one might outline an operator that explicitly accounts for all many-body interactions between the inactive and energetic subsystems, although most likely, this is able to lead to a technique that’s computationally as costly as fixing straight your complete downside with such an strategy. Due to this fact, in follow, the embedding potential introduces approximations to explain the low-energy levels of freedom and the interactions between energetic and inactive subsystems. For instance, one such choice could be to make use of the Hartree-Fock (HF) approximation for the inactive electrons, such that the energetic electrons solely work together with the inactive ones in a mean-field method. On this case, ({V}_{uv}^{,textual content{emb},}) would merely correspond to the weather of the Fock matrix. Equally, as we are going to talk about in additional element within the subsequent part, describing the atmosphere utilizing DFT interprets into an embedding potential just like the Kohn-Sham (KS) one. It is very important notice that, on the whole, ({V}_{uv}^{,textual content{emb},}) all the time will depend on the inactive digital levels of freedom, however presumably additionally on the energetic subsystem, through which case the ensuing embedding scheme must be solved self-consistently (see Fig. 2).

The left column depicts the qualitative molecular orbitals of a water molecule. The fitting column depicts the molecular orbitals localized across the positively charged boron emptiness in hexagonal boron nitride. In each circumstances, solely a small variety of orbitals is included within the energetic area: for water, it’s spanned by the HOMO-LUMO pair, whereas for boron nitride, by the localized defect orbitals.

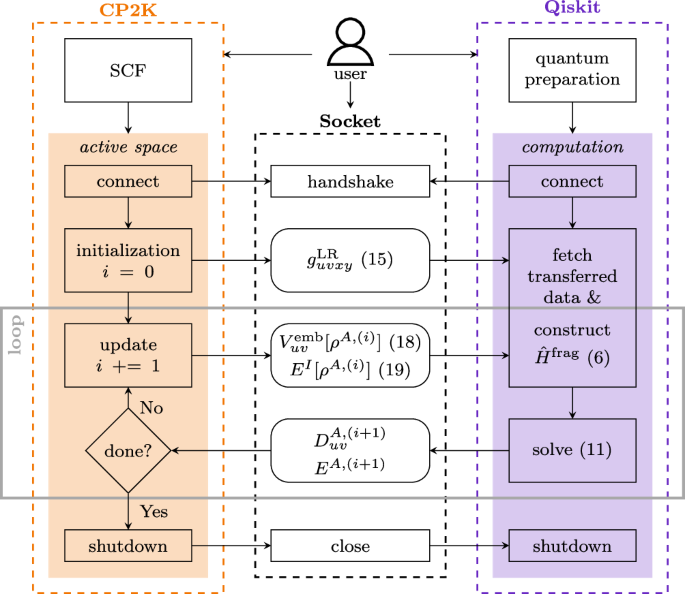
The person configures the 2 classical processes and the socket for the IPC. Every course of then follows the computational steps (rectangular packing containers) outlined inside their respective frames. The information that will get computed and transferred is indicated by the rounded packing containers. Numbers in parentheses confer with the respective equations on this manuscript. The self-consistent embedding requires a loop which is highlighted by the grey field. This loop is terminated primarily based on the choice (diamond form) taken by the CP2K course of.

To compute the whole power of the system, we will begin from the expectation worth of Eq. (1) with respect to the whole WF of the system, that’s

the place

are the weather of the one- and two-particle diminished density matrices (RDMs), D and d, respectively. By separating the one-particle RDM (1-RDM) into inactive and energetic elements, D = D^I + D^A, and factorizing the weather of the inactive two-particle RDM (2-RDM) right into a product of 1-RDMs (see Appendix A.1 and A.2 of Rosssmannek et al.⁵ for an in depth derivation), we will categorical the whole power as a sum of inactive and energetic elements, E = E^I + E^A, with

and

In Eq. (10) and (11), the indices i, j label inactive orbitals, and the superscripts I and A on the density-matrix parts emphasize to which subspace they belong (despite the fact that the indices and sums implicitly account for that data). Eventually, discover that the selection of one-particle features is totally common: one can select localized molecular orbitals within the case of molecules, crystalline orbitals, or Wannier features in solid-state programs, or a mix thereof, e.g., to explain level defects in supplies.

To increase the formalism to periodic range-separated DFT embedding, the primary ingredient is the definition of the one-particle embedding potential, with parts

the place the weather of the inactive long-range Fock operator are outlined as

together with the classical Hartree potential, V_H[ρ], the precise Hartree-Fock trade potential, V_HFX[ρ], and the DFT exchange-correlation potential, V_xc[ρ], evaluated over the indicated electron densities, ρ^I, ρ^A and ρ = ρ^I + ρ^A (see the Supplementary Information (SI) for the specific definition of those operators in a one-particle foundation). The 2-electron integrals over the Coulomb operator are cut up into long-range (LR) and short-range (SR) elements,

which give rise to the superscripts LR and SR in Eqs. (12) and (13). The vary separation is obtained with the error perform and its complement (as indicated by Eq. (15)), the place ω is the range-separation (RS) parameter of models ({a}_{0}^{-1}).

In follow, two points come up for the direct computation of the inactive power and embedding potential in response to Eqs. (10) and (12). First, it’s computationally disadvantageous when the inactive subsystem turns into very massive. Second, for periodic calculations, the sums in regards to the electron-electron, electron-nuclear, and nuclear-nuclear interactions are conditionally convergent, and can’t be simply separated into inactive and energetic elements. Therefore, we categorical the inactive phrases not directly because the distinction between the whole system and the (localized) energetic subsystem. We are able to obtain this by defining the inactive 1-RDM and electron density as D^I = D − D^A and ρ^I = ρ − ρ^A, respectively. Reformulating Eq. (13) by changing ρ^I = ρ − ρ^A, yields

the place the whole rsDFT Fock operator is outlined as

Inserting the identical relation for the inactive electron density in addition to Eq. (16) into Eq. (12) ends in

We are able to proceed analogously for the expression of the inactive power, acquiring

The energetic power element that’s wanted to compute the whole power, E = E^I + E^A, merely corresponds to the bottom state of the fragment Hamiltonian, Eq. (6). Owing to the same construction of Eqs. (1) and (6) primarily any digital construction methodology can be utilized together with our embedding scheme. In follow, as a result of the area spanned by the energetic orbitals and electrons is comparatively small, precise diagonalization or a superb approximation thereof is the strategy of selection. Electronically excited states can be focused by the embedding methodology, both by straight calculating the spectrum of ({hat{H}}^{{rm{frag}}}) or by linear response. Nevertheless, one must be cautious that the inactive subspace is generally optimized for the bottom state, except some type of state-averaging or orbital optimization just like classical multiconfigurational quantum chemical strategies is launched^26,27. As will likely be mentioned within the subsequent part, now we have used quantum circuit ansatzes to acquire the bottom and excited states energies of Eq. (6). Owing to the dependence of the embedding potential to the AS electron density, ρ^A, the strategy chosen to get the spectrum of ({hat{H}}^{{rm{frag}}}) must also present this amount (extra typically, it ought to present the 1-RDM). Crucially, this dependence of V^emb on ρ^A implies that our embedding strategy requires a self-consistent resolution, whereby an up to date energetic density is obtained at every iteration, which is used to construct a refined embedding potential and up to date inactive power that accounts for the suggestions of the energetic subsystem on the atmosphere levels of freedom. A scheme depicting this self-consistent loop is proven in Fig. 2, when discussing the implementation particulars within the part “Quantum-classical interface implementation”.

Lastly, it ought to be emphasised that Eqs. (18) and (19) are legitimate for each the molecular and periodic embedding settings, at the very least when invoking the Γ level approximation, since solely the computation of the whole Fock operator and power are affected by this alteration. Therefore, in follow, the introduced methodology is a generalization of multiconfigurational rsDFT to periodic programs sampled on the Γ level. Moreover, we level out the limiting circumstances offered by the RS scheme: they permit us to get well the widespread HF embedding scheme (i.e., full energetic area configuration interplay) as ω approaches infinity in addition to KS-DFT as ω approaches zero. This may be seen in Eqs. (18) and (19), the place the usual KS case is clear as all LR phrases merely disappear. The widespread HF embedding can also be evident from Eq. (17), through which the one DFT-specific time period for the exchange-correlation interplay, ({V}_{xc}^{,textual content{SR},}), vanishes.

Quantum-classical interface implementation

On this part, we current the implementation particulars of the combination of CP2K¹⁴ and Qiskit Nature^15,16. The developments of this work have been launched as a part of CP2K v2024.1, Qiskit Nature v0.7.0, in addition to a separate module dealing with extra particular elements of the combination referred to as qiskit-nature-cp2k²⁸. Within the first half, we talk about the technical features and challenges. Later, we evaluation the longer term scalability and extensibility of this design.

Interfacing CP2K with Qiskit Nature for the implementation of an iterative embedding scheme poses quite a few challenges. Whereas CP2K is primarily written in Fortran and offers the means to effectively run extremely parallelized simulations in quite a lot of computational setups, Qiskit Nature (and the underlying Qiskit Qiskit software program growth equipment (SDK)) is usually developed in Python and has not but (on the time of writing) reached a computational maturity corresponding to CP2K. When Qiskit Nature was coupled to different Python-based computational applications up to now, they may simply share the identical Python runtime execution atmosphere and, thus, share all knowledge straight in reminiscence^5,13. For the combination mentioned right here, this was not potential in such a simple method. As a substitute, our implementation depends on a message passing protocol so as to trade knowledge between the 2 codes. Significantly, for this preliminary implementation, the messages and knowledge are despatched over a socket file. That is impressed by an analogous structure utilized by the i–Pi challenge²⁹. Extra technical particulars can be found within the SI.

A socket is an software programming interface (API) used for inter-process communication (IPC). Utilizing this protocol, it’s potential for the speaking processes to run on the identical bodily machine or totally different ones related through the web. The calculation proceeds identically in each situations, with the one distinction being the latency of the communication. Nevertheless, this isn’t of concern to us, because the rate-limiting issue of the communication is (in any case) the bandwidth of the connection to the quantum {hardware}. That is additionally a motive for the selection of utilizing the socket API for the communication moderately than a tighter integration of the 2 codes utilizing ctypes. Whereas the latter is prone to have a efficiency benefit, the benefit of additional implementations to couple to different codes outweighs. Moreover, the computation of the AS resolution can also be prone to outweigh the price of communication.

Determine 2 summarizes the computational workflow of our integration between CP2K and Qiskit Nature. The diagram depicts a person who has to configure three elements of their calculation; the CP2K and Qiskit (Nature) processes depicted on the left and proper, respectively, in addition to the socket itself through which the messages are handed between the 2 codes. Each computational codes will begin in parallel. Whereas CP2K begins out by discovering a low-level resolution to your complete system (SCF), Qiskit can use this time to carry out sure preparational duties which can be distinctive to the execution of quantum computing {hardware} and don’t require problem-specific knowledge. For each applications, the person has full flexibility to leverage their respective capabilities throughout these preliminary steps. Upon completion of their respective steps, each codes will synchronize by performing a handshake by the socket. If both course of reaches this level earlier than the opposite, it awaits the opposite one. CP2K reaches this level inside its energetic area module, which was launched as a part of CP2K v2024.1. The enter to this module configures the energetic fragment to be embedded into its atmosphere and computes the one- and two-body phrases of the AS Hamiltonian (i.e., the fragment Hamiltonian). It permits each single-shot and iterative embedding routines to be carried out. In Fig. 2 now we have depicted the ultimate rsDFT embedding protocol. Nevertheless, a number of the elements don’t change all through the course of the self-consistent embedding. These might be pre-computed solely as soon as through the initialization process. A key instance is the LR-electron-repulsion integrals (ERIs) (cf. Eqs. (3) and (15)). Due to this fact, these solely must be transferred to the Qiskit course of as soon as. Elements that rely upon the energetic density of the present iteration, ρ^A,(i), must be up to date and exchanged throughout each iteration of the loop indicated by the grey body in Fig. 2. Throughout each such iteration, Qiskit Nature constructs the Hamiltonian of the energetic fragment (cf. Eq. (6)) utilizing the LR-ERIs and embedding potential, ({V}_{uv}^{,textual content{emb},}[{rho }^{A,(i)}]), (cf. Eq. (18)). It then proceeds with discovering the ground-state resolution to this Hamiltonian utilizing the quantum circuit ansatz specified by the person. Upon completion, it would return the energetic power, E^A,(i+1), and energetic 1-RDM, ({D}_{uv}^{A,(i+1)}), to the CP2K course of. CP2K will then carry out a convergence test primarily based on the whole power, E = E^I + E^A,(i+1). If convergence has not been reached, CP2K and Qiskit will return again to their respective steps of the embedding protocol to proceed with one other iteration. If this test succeeds, each processes will likely be signaled to terminate. Throughout their shutdown procedures, each processes might carry out extra post-processing steps. For instance, Qiskit Nature might compute extra properties utilizing the ultimate ground-state WF together with the computation of excited-state energies.

At this level one may marvel how scalable this design is for the longer term. Certainly, the switch of the two-body integrals is the limiting issue right here. If CP2K and Qiskit Nature have been capable of leverage a shared reminiscence, this is able to alleviate the necessity for switch utterly. Nevertheless, solely as much as the purpose the place the mapped qubit Hamiltonian must be transferred to the QPU (quantum processing unit). Till now we have a direct high-bandwidth connection between the CPU and QPU, this switch of knowledge will stay the rate-limiting issue. Due to this fact, inside the scope of this extra common downside, we deem the present implementation and design as scalable. Moreover, future enhancements to assist within the switch of knowledge to the QPU that will likely be carried out into the quantum stack will likely be accessible on to the end-users of our integration as a result of it solely serves as a intermediary between the 2 codes.

As soon as once more, we emphasize that the introduced structure offers a common framework for the implementation of energetic area embedding approaches. From a software program perspective, any two codes could also be coupled through the described interface. From a theoretical perspective, it’s simple to implement different embedding approaches into an current implementation. For instance, a projection-based embedding strategy reminiscent of this earlier work by a number of the authors¹³ can merely be carried out by including a brand new subroutine to CP2K to compute the embedding potential with out requiring any additional modifications to the combination protocol or the AS solver.

Optical properties of the oxygen emptiness in MgO

To check our implementation now we have studied the optical properties of the F⁰-center (impartial oxygen emptiness) in magnesium oxide, whose nature stays unclear regardless of the numerous experimental^30,31,32,33 and computational^{34,35,36,37,38,39,40,41} research carried out up to now many years. This knowledge will enable us to match the accuracy of the periodic rsDFT embedding with respect to each experimental spectra in addition to state-of-the-art ab initio strategies.

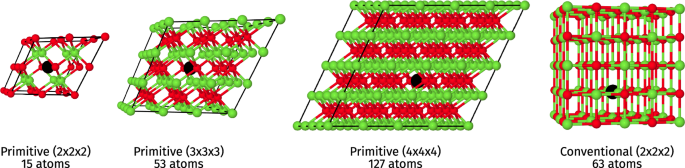
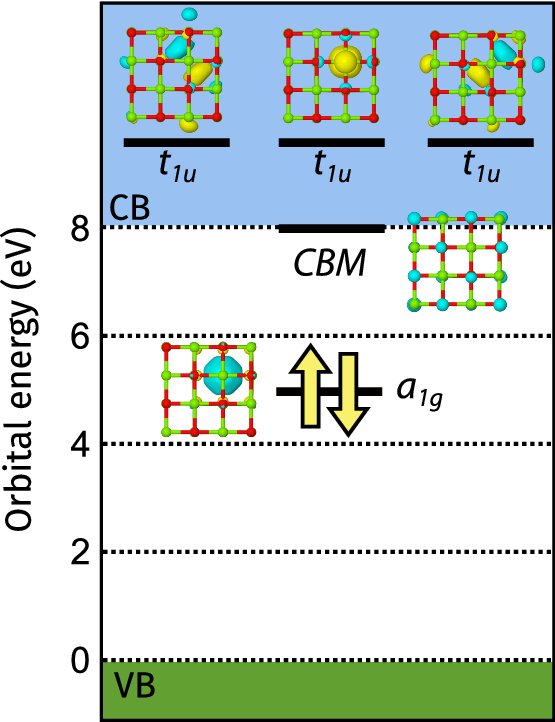
We now have thought-about 4 totally different supercell sizes: the two × 2 × 2, 3 × 3 × 3 and 4 × 4 × 4 supercells constructed from the primitive unit cell, and the two × 2 × 2 supercell constructed from the standard unit cell; see Fig. 3. The embedding calculations have been carried out by together with 2 electrons and 5 orbitals (10 spin-orbitals in whole) within the AS, that are proven inside the band construction diagram in Fig. 4 (and are reproduced with larger decision within the SI). 4 of the 5 energetic orbitals are localized on the emptiness and are labeled in response to the (localized) octahedral symmetry across the defect (O_h level group). The remaining orbital included corresponds to the conduction band minimal (CBM) and is a completely delocalized conduction s-band, which we label as CBM within the following. The bottom state power of the embedded fragment Hamiltonian was obtained utilizing the variational quantum eigensolver (VQE) algorithm⁴ with a quantum unitary coupled cluster singles and doubles (q-UCCSD) ansatz⁴², and the excited states have been obtained utilizing the quantum equation of movement (qEOM) strategy⁴³. A quick evaluation of crucial quantum computing ideas is offered within the part “Quantum computing”, together with detailed data on the computational settings used for these calculations in part “Computational particulars”.

Magnesium atoms are in inexperienced, oxygen atoms are in pink, the oxygen emptiness is coloured in black.

The closed-shell A_1g singlet-spin floor state is depicted, with two electrons occupying a defect orbital labeled a_1g inside the hole. Singlet and triplet excitons happen when an electron from the mid-gap orbital is happy both to the absolutely delocalized CBM state or to one of many three t_1u defect orbitals inside the conduction band (CB).

A impartial oxygen emptiness in MgO introduces a 1 s-type localized defect orbital at mid-gap that’s doubly occupied within the ¹A_1g digital floor state. We will name this orbital the mid-gap orbital. Three extra defect-localized degenerate one-particle states of t_1u symmetry (p-like orbitals) seem inside the conduction band. These three orbitals are energetically barely above the CBM, which corresponds to the delocalized s-band. The 4 orbitals localized on the oxygen emptiness and the CBM one are proven in Fig. 4 and are believed to be accountable for the optical properties of faulty MgO; for that reason, we included them within the energetic area of our embedding calculation, together with the two electrons occupying the mid-gap defect state.

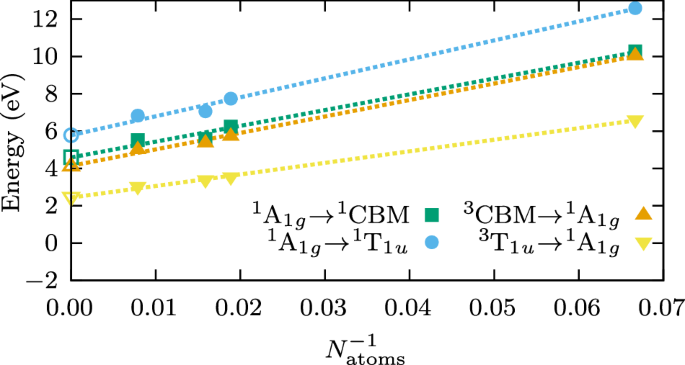
Experimentally, it’s effectively established that the absorption peak of the F⁰-center is at 5.03 eV, which is extraordinarily near that of the F⁺-center (that’s, a positively charged oxygen emptiness) at 4.96 eV^30,31. We recognized the vertical excitation energies akin to the transition of 1 electron from the mid-gap orbital to both the CBM or the t_1u orbitals, denoted as ¹A_1g → ¹CBM and ¹A_1g → ¹T_1u, respectively. In Fig. 5, we present in blue and inexperienced the energies obtained for these states as a perform of the variety of atoms within the supercell. Discover that the energies calculated with our embedding methodology are obtained straight from many-body wave features, thus they account for electron-hole interactions and the exciton binding power. We carried out an extrapolation to the thermodynamic restrict (TDL) assuming a ({N}_{textual content{atoms}}^{-1}) convergence to appropriate for finite-size results, which is proven as dashed strains in Fig. 5. Our greatest estimates are reported on the backside of Desk 1, together with all of the energies obtained for the totally different supercell sizes. The transition to the ¹CBM state is predicted to be 4.60 eV, whereas for the (triply degenerate) one to the ¹T_1u state, we get 5.78 eV. The experimental absorption peak at 5.03 eV corresponds to the ¹A_1g → ¹T_1u, because the excitation to the CBM is dipole-forbidden; we, due to this fact, overestimate the experimental worth by 0.75 eV. This end result might be in comparison with quite a few different computational research on the F⁰-center in magnesium oxide, which have been carried out with a big number of strategies from each the solid-state physics and quantum chemistry communities. From Desk 2 we will see that many of the quantum chemistry strategies overestimate the absorption to the localized ¹T_1u state, whereas FN-DMC³⁶ and G₀W₀-BSE³⁵ reproduce the experimental absorption peak, even if they doubtless goal the CBM state moderately than the defect one. This may increasingly recommend that the transition to the ¹T_1u obtained with these strategies is presumably overestimating the experimental absorption most. Our calculations persistently predict a blue-shifted absorption by ~0.5 eV in comparison with the embedded-BSE@DDH of Vorwerk et al.³⁹. Whereas usually, the small (2,5) AS might be a motive for this, the AS convergence research reported within the SI suggests in any other case, as just about the identical outcomes are obtained with 8 electrons in 60 orbitals. We, due to this fact, ascribe the blue-shift to the shortage of orbital rest within the atmosphere, which is optimized for the bottom state solely. In passing, we additionally notice that the noticed weak dependence on the energetic area measurement in our calculations is because of the RS parameter used on this work, (omega =0.14{a_0^{-1}}). A bigger worth of ω would enhance the significance of the energetic area measurement, as proven within the SI for (omega =0.4{a_0^{-1}}), highlighting the sensitivity of the strategy to the worth used for the RS parameter. Due to this fact, you will need to select an energetic area that’s not solely related to the bodily downside at hand, however that can also be converged with respect to the worth of ω. A extra detailed dialogue about that is obtainable within the part “Strategies” of the SI. Curiously, density-matrix embedding principle⁴⁰ predicts the absorption to the CBM state to be larger than the one to the localized state, maybe owing to the lacking extrapolation to the TDL. The one methodology that underestimates the absorption is TDDFT, with an absorption peak centered at 4.85 eV³⁷.

Stuffed inexperienced squares and blue circles correspond to calculated singlet absorption energies, whereas stuffed upside-orange and downside-yellow triangles correspond to calculated triplet emission energies. Dashed strains are linear extrapolation curves to the TDL, whose worth is marked with a corresponding empty image.

The photoluminescence (PL) of faulty MgO is significantly extra difficult than the absorption, and a number of other interpretations have been introduced ahead all through the years. The principle supply of ambiguity is the neighborhood of the absorption peaks of the F⁰, F⁺, and F²⁺ facilities, that are all prone to be excited by incoming irradiation at 5 eV, considerably complicating the project of the emission bands to the proper level defect and digital state. Experimentally, there are two very distinct peaks seen within the PL spectrum, one at 2.3 eV and one at 3.2 eV^32,33. The previous has been related to an emission from the F⁰-center, whereas the latter to an emission from the F⁺-center^32,33. The preliminary clarification for the long-lived nature of the two.3 eV band was primarily based on temperature-dependent experiments carried out on samples ready in several methods and containing totally different concentrations of F⁰-centers and hydrogen impurities. The proposed mechanism entails the escape of an electron within the conduction band upon excitation of the F⁰-center, forsaking a positively charged oxygen emptiness, an F⁺-center. Hydrogen impurities within the pattern then act as traps for the cellular electrons, which can be thermally launched again at a later time into the conduction band. Two processes can occur with the launched electrons: they might encounter F⁺-centers left behind after the absorption course of, through which case they recombine in an excited ¹T_1u state of the F⁰-center that shortly emits mild, or they might be recaptured by H⁻ traps, slowing down the general emission course of. Another, extra simple interpretation is that the emission band is solely attributable to triplet phosphorescence from a localized ³T_1u state on the defect, accessed through inter-system crossing from the excited ¹T_1u state. This second interpretation is probably the most accepted clarification in current computational research, corroborated by calculations primarily based on superior ab initio methodologies^37,38,39,40 (in distinction to the primary interpretation primarily based on older semi-empirical strategies and experiments^32,33).

In mild of this evaluation, we additionally examine the second pathway because the main emission course of and compute the photoluminescence from the relaxed ³T_1u construction and state. Our outcomes are proven by the orange and yellow strains in Fig. 5 and listed in Desk 3. The expected worth for the emission from the localized triplet state is 2.44 eV and is in excellent settlement with the experimental worth of two.3 eV. Particularly, we’re a lot nearer to this worth than different methodologies, which persistently predict larger energies for this emission band as proven within the final column of Desk 2. The higher accuracy of this worth with respect to experiment in comparison with the singlet excitation power obtained for the absorption to the ¹T_1u state is probably going because of the relaxed inactive orbitals, which have been optimized for this state within the reference SR native density approximation (LDA) SCF calculation. These ought to present a greater embedding potential in comparison with that for the excited singlet state, whose inactive orbitals have been optimized for the closed-shell floor state. Nonetheless, one must be cautious when evaluating totally different theoretical works, since these targeted on totally different states or mechanisms. The work by Vorwerk et al.³⁹ reported 2.93 eV because the PL from the F⁺-center, therefore to be in contrast with the experimental worth of three.2 eV. The sooner work primarily based on FN-DMC³⁶ and G₀W₀-BSE³⁵ reported the emission from the singlet state (whether or not the CBM or T_1u state is unclear), and have concluded that the project from the experimental research ought to be re-evaluated, with the three.2 eV peak assigned to the F⁰-center moderately than the F⁺ heart. All of the works utilizing approaches primarily based on quantum chemistry strategies, that’s NEVPT2-DMET, EOM-CCSD, TDDFT, and CASPT2, analyze the transition ³T_1u → ¹A_1g like us and examine their outcomes in opposition to the two.3 eV band^34,37,38,40. Right here, we do the identical, and we get the perfect theoretical end result up to now, which corroborates the experimental project of the two.3 eV band to the F⁰-center, although originating from a special mechanism than the initially proposed one. Whereas this isn’t conclusive proof, the competing interpretation depends on emission from the singlet state, ¹T_1u → ¹A_1g, which is generally anticipated to be larger in power than the corresponding triplet one, therefore additional away from the experimental worth.