Deep Bayesian active learning using in-memory computing hardware

Synapse weights stochastic traits

To implement in-memory DBAL, we used an expandable stochastic CIM computing (ESCIM) system (Prolonged Information Fig. 1). The ESICM system, expandable via stacking, built-in three memristor chips on this examine. The memristor system adopted the TiN/TaO_x/HfO_x/TiN materials stack. Determine 2a depicts the present–voltage (I–V) curves of the 1-transistor-1-memristor (1T1R) cell, that are clean and symmetrical. Because of TaO_x, which serves as a thermally enhanced layer³³, the multilevel traits of the memristor are improved.

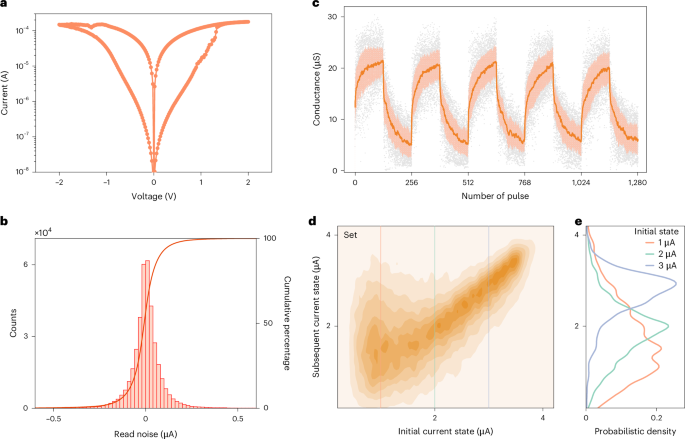
a, A typical measured I–V curve of a single 1T1R cell for a quasi-d.c. sweep. b, The chance density of the learn noise within the 3.3 μA present state at learn voltage V_learn = 0.2 V, measured over 1,000 learn cycles throughout particular person arrays. c, Typical analog switching behaviors of memristors below equivalent pulse trains. The darkish traces characterize the typical values of the conductance, the sunshine colours fill the areas between plus and minus one normal deviation, and the grey dots characterize measured information. d, The statistical distribution of the conductance transition from their preliminary states to states for units in a 4K chip, below a single set pulse with constant-amplitude voltage V_set = 2.0 V. The gate voltage of the transistor is V_t = 1.25 V. The present state is measured at learn voltage V_learn = 0.2 V. e, Likelihood density curves of the conductance transition at three preliminary states (I_learn = 1 μA, 2 μA and three μA). Every curve corresponds to a profile alongside the vertical traces proven in d.

Source data

To research the stochastic traits of the memristor, we measured conductance variations in the course of the studying and modulation course of. On the one hand, the fluctuation information collected from the studying check will be modeled utilizing a double exponential distribution (Fig. 2b). Memristors in several present states have distinct random fluctuation traits (Prolonged Information Figs. 2 and 3). The measured outcomes of learn noise align nicely with the earlier reviews of present fluctuation behaviors in HfO_x-based memristor units^34,35 (Supplementary Be aware 1). By adjusting the memristor to an applicable present state, numerous chance distributions will be obtained (‘In situ sampling by way of studying memristors’ part in Methods). Such distinctive stochastic traits can facilitate in situ random quantity era by studying the present. Based on the Lindeberg–Feller central restrict theorem (Supplementary Be aware 2), the Gaussian distribution will be realized by accumulating the currents of a number of memristors (Prolonged Information Fig. 4). Therefore, the ESCIM system can effectively carry out each in situ Gaussian random quantity era and in-memory computation, integrating the units and cycles variabilities of memristors (Prolonged Information Fig. 5 and Supplementary Be aware 3).

Alternatively, memristors even have random fluctuations in the course of the conductance modulation course of. Beneath identical-amplitude voltage pulse modulation, the memristor displays steady bidirectional resistive switching traits (Fig. 2c). In the meantime, random migration of oxygen ions inside the resistive layer could cause variations impacting the conductance of various units, even inside the similar system throughout cycles. To quantitatively analyze these inherent stochastic traits, we measured conductance transitions (‘Measurements of the conductance transition’ part in Methods). We utilized a constant-amplitude voltage pulse to the 1T1R cells, prompting the memristors to transition from preliminary to subsequent conductance states. Determine 2d reveals the conductance transition distribution in the course of the set operation. Whereas the next conductance usually will increase throughout a set operation, decreases can happen on account of random oxygen ion migration. Moreover, the unfold of the transition distribution varies relying on the preliminary conductance state. Determine 2e reveals the transition chance curves for 3 completely different preliminary conductance states, clearly exhibiting an alignment with a Gaussian distribution. As well as, the conductance transition within the case of reset operation additionally displays an analogous Gaussian distribution (Prolonged Information Fig. 6). Subsequently, the operation of a single pulse throughout a memristor’s conductance modulation will be modeled as drawing a random quantity from a Gaussian distribution.

In-memory DBAL

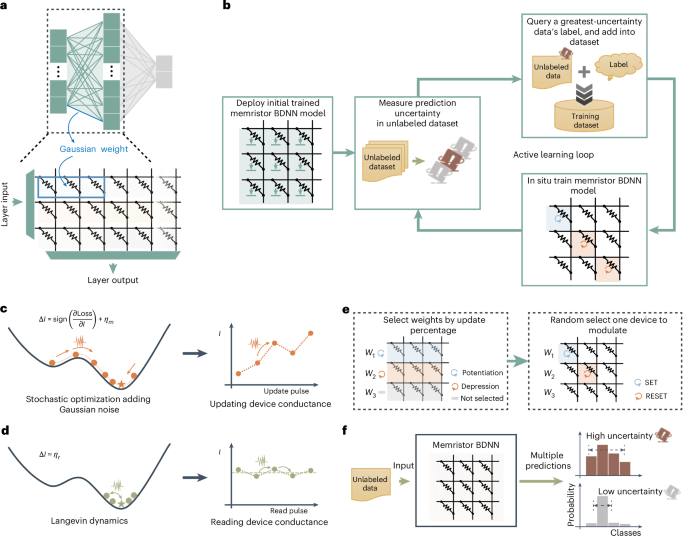
In line with the Lindeberg–Feller central restrict theorem, Gaussian weights in a BDNN will be simulated utilizing learn currents from a number of units (Fig. 3a). Inside our implementation technique, a Gaussian weight is produced utilizing three units within the ESCIM system. As proven in Fig. 3b, we proposed the in-memory DBAL framework constructing on a memristor BDNN (Supplementary Be aware 4).

a, Realization of a Gaussian weight of a BDNN in memristor crossbar array. Learn currents amassed from three units act as one Gaussian weight. b, The proposed in-memory Bayesian energetic studying movement chart. c, The preliminary section of the proposed mSGLD. The conductance of the memristor is up to date in line with the signal of the gradient to imitate an efficient stochastic gradient studying algorithm. The added Gaussian noise η_m will be realized by the random fluctuations of conductance modulation course of. d, The latter section of the proposed mSGLD. The community optimization course of got here right into a flat minimal of the loss perform, and the magnitude of the gradient diminished. Gaussian noise of the overall learn present dominates, thus mimicking the Langevin dynamic MH course of. e, Realization of the load updating. Left: a sure proportion of weights with giant gradient magnitude is chosen to be up to date, and this replace ratio retains reducing with the variety of coaching iterations. Proper: one of many three units of those chosen weights is randomly chosen for modulation to comprehend the load replace. f, By making a number of predictions, the prediction distribution will be effectively obtained and, thus, the uncertainty will be calculated.

The proposed in-memory DBAL framework integrates a digital laptop and our ESCIM system (Prolonged Information Fig. 7). First, an preliminary memristor BDNN mannequin is deployed on memristor crossbar arrays (for the pseudocode, discuss with Supplementary Fig. 1). This mannequin’s weights are obtained by ex situ coaching on a digital laptop utilizing a small preliminary coaching dataset. The learn noise mannequin and conductance modulation mannequin are used throughout this course of, enabling the community to study weight distributions that higher match the built-in memristor arrays (‘Stochastic fashions of memristors’ part in Methods). Subsequent, the deployed memristor BDNN predicts the courses of knowledge within the unlabeled dataset (Supplementary Fig. 2), and calculates prediction uncertainty (Supplementary Fig. 3). This course of includes absolutely turning on the transistors within the crossbar array, making use of the learn voltage to the supply line (SL) of the system row by row and sensing the fluctuating learn present that flows via the digital floor BL by an analog-to-digital converter (ADC). The community prediction, as a result of weight’s stochasticity launched by the memristor cells’ variabilities, is a distribution reflecting the variability in learn currents relatively than a single deterministic worth (‘Uncertainty quantification’ part in Methods). Consequently, we are able to use the a number of prediction outputs from the community to derive a prediction distribution, thereby calculating the prediction uncertainty. Subsequently, based mostly on the prediction uncertainty of the samples within the unlabeled dataset, we choose an information pattern with the best uncertainty to question for its label and incorporate this pattern and the queried label into the coaching dataset. A knowledge pattern with the best uncertainty usually comprises extra data, and its label is mostly probably the most helpful for enhancing the community’s classification efficiency. Lastly, utilizing the up to date coaching dataset, which incorporates the unique coaching information and the newly added samples, the memristor BDNN performs in situ studying. After in situ studying, the community continues to calculate uncertainty, choose high-uncertainty samples and retrain till efficiency expectations are met or label queries are exhausted.

Within the strategy of energetic studying, the in situ studying step is essential. Given the restricted amount of samples within the coaching dataset, insufficient in situ studying capability may result in a community with poor classification capabilities. This would possibly hinder the quantification of uncertainty, thereby difficult the identification of helpful unlabeled information samples. Even after a number of rounds of energetic studying, the community efficiency would possibly nonetheless not meet the anticipated requirements.

In situ studying to seize uncertainty

To precisely seize uncertainty in DBAL’s iterative studying, we proposed an in situ studying methodology utilizing the stochastic property of the conductance modulation course of (Supplementary Fig. 4). The strategy is an enchancment based mostly on the stochastic gradient Langevin dynamics (SGLD) algorithm¹⁶. The burden parameter replace within the SGLD algorithm may be very easy: it takes the gradient step of conventional coaching algorithms³⁶ and provides an quantity of Gaussian noise. The coaching strategy of SGLD consists of two phases. Within the preliminary section, the gradient shall be dominant and the algorithm will mimic an environment friendly stochastic gradient algorithm. As step sizes decay with the variety of coaching iterations, within the latter section, the injected Gaussian noise shall be dominant and, subsequently, the algorithm will mimic the Langevin dynamic Metropolis–Hastings (MH) algorithm. Because the variety of coaching iterations will increase, the algorithm will easily transit between the 2 phases. Utilizing the SGLD methodology permits the load parameters to seize parameter uncertainty and never simply collapse to the utmost a posteriori answer.

Primarily based on the stochastic nature of memristors, we improved the SGLD algorithm utilizing signal backpropagation, particularly, mSGLD. The stochastic fluctuation below constant-amplitude pulses may also be thought of as random quantity era. Within the preliminary section of mSGLD, we calculated the gradient of the memristor conductance (frac{partial {{mathrm{Loss}}}}{partial I}) (‘mSGLD coaching methodology’ part in Methods) after which up to date the worth of the memristor weight based mostly on the signal of the gradient to imitate an efficient stochastic gradient studying algorithm

For the reason that transition chance of the conductance throughout modulation is Gaussian distribution, the added Gaussian noise η_m will be realized by the random fluctuations inherent within the system (Fig. 3c). Subsequently, the precise replace operation of the system on the memristor array is

That’s, if the signal of the gradient of a tool is optimistic, a set operation is carried out on the system; whether it is adverse, a reset operation is carried out.

Within the later section of mSGLD, with extra coaching iterations, the memristor community’s classification efficiency improves. Because it reaches a flat loss perform minimal, the gradient diminishes and injected Gaussian noise turns into dominant (Fig. 3d). For clean transition between the 2 phases, we proposed a clean transition methodology. On this methodology, we replace a reducing proportion of weights with giant gradients as coaching iterations enhance (‘mSGLD coaching methodology’ part in Methods and Prolonged Information Fig. 8). Then, for the chosen weights, one among three units is randomly chosen for modulation to replace the load (Fig. 3e). Subsequently, because the variety of coaching iterations will increase, the coaching ends and the variety of up to date weights decreases to a small quantity. Lastly, the Gaussian noise of the overall learn present dominates, thus mimicking the Langevin dynamic MH course of. By progressively reducing the load replace ratio, the sleek transition between phases additionally reduces the adverse impression of extreme conductance stochasticity, stabilizing the community studying course of. We additionally totally focus on administration of noise in mSGLD (Supplementary Figs. 5 and 6), utilizing common SGD as an alternative of mSGLD (Supplementary Fig. 7), and the impression of binarizing the gradient (Supplementary Fig. 8) in a BDAL simulation experiment based mostly on a Modified Nationwide Institute of Requirements and Know-how (MNIST) dataset classification job. The outcomes present the effectiveness and resilience of our proposed mSGLD methodology (Supplementary Be aware 5).

Our proposed in situ studying algorithms leverage stochastic traits within the studying and conductance modulation course of for Gaussian random quantity era throughout community prediction and studying. In BDNN studying, weights are up to date with gradient values added Gaussian noise, permitting Bayesian parameter uncertainty seize by way of the in situ mSGLD methodology. In BDNN prediction, Gaussian weights are sampled and computed via VMM with the enter vector. Memristor Gaussian weights in crossbar arrays allow environment friendly weight sampling and VMM with a single learn operation. A number of predictions yield the prediction distribution and calculate uncertainty (Fig. 3f).

Robotic’s ability studying

To exhibit the applicability of the proposed strategies, we carried out an illustration in a robotic’s ability studying job (Fig. 4a). On this studying job (‘Robotic’s pouring ability studying job and robotic simulator’ part in Methods), the robotic is provided with a set of fundamental talents corresponding to locomotion and fundamental object manipulation. The robotic must construct on these foundations by coaching a BDNN mannequin to accumulate pouring high-level abilities. Nonetheless, the labeled information required to study the ability are very troublesome, time-consuming or costly to acquire on account of useful resource overhead and time overhead. Subsequently, the robotic must effectively study the pouring ability with as few labeled samples or makes an attempt as attainable, thus minimizing the experiments time, labor and value for acquiring labeled information.

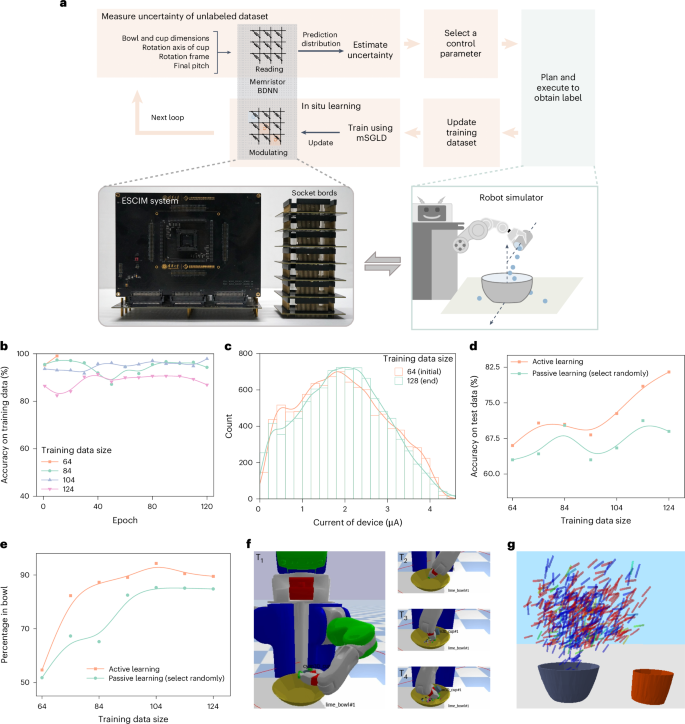
a, A schematic illustration of robotic’s pouring ability studying job utilizing in-memory DBAL. b, The evolution of the accuracy on coaching information of the memristor BDNN with every epoch on 64, 84, 104 and 124 coaching dataset sizes. c, Histogram (bar) and distribution curve (line) of memristor conductance state on the preliminary and finish of the energetic studying loop. Measured at learn voltage V_learn = 0.2 V. d, The classification accuracy on the check dataset of the energetic studying methodology and the passive studying methodology. Energetic studying has a bonus in contrast with passive studying, which randomly selects the samples to be queried. e, The educational efficiency of energetic and passive studying strategies. We used the share of pouring the contents of the cup into the bowl as a efficiency metric. f, Visualization of the energetic studying outcomes. The robotic is pouring the beads from the cup into the bowl. T₁, T₂, T₃ and T₄ characterize sequential time factors within the strategy of pouring. g, Visualization of the ultimate cup place for 500 pour legitimate management parameters. It visualizes probably the most assured (low uncertainty) prediction of the memristor BDNN by coloring small values in crimson and enormous values in blue.

Source data

The anticipated impact of the pouring motion is to pour the contents of a cup right into a bowl. We’re eager about studying below what constraints the execution of this motion will switch a sufficiently giant portion of the preliminary contents of the cup into the goal bowl. These constraints for a pour are the context parameters (the bowl and cup dimensions) and management parameters that the robotic can select (the axis of rotation, the cup rotation body and the ultimate pitch). To execute profitable pouring motion, we used a memristor BDNN to foretell whether or not the execution of the pouring motion shall be profitable or not below completely different management parameters after which proceed to the following step of plan and execution based mostly on the management parameters which have the next chance of success (Fig. 4a). Thus, our essential goal is to coach a BDNN to realize excessive accuracy and motion effectiveness utilizing as few labeled samples as attainable, via the proposed energetic studying strategies.

We applied an energetic studying job utilizing an 11 × 50 × 50 × 2 memristor BDNN (‘Experiment system setup’ part in Methods), balancing {hardware} complexity and community efficiency (Supplementary Be aware 6). The BDNN was educated on a digital laptop utilizing a 64-sample dataset, then deployed to the ESCIM system. Within the energetic studying loop (Fig. 4a), the memristor BDNN predicts and estimates uncertainties of 10,000 unlabeled constraints, queries the label of probably the most unsure constraint and provides it to the coaching set. The memristor BDNN then makes use of the up to date dataset for 110 epoch iterations of in situ studying by way of the proposed mSGLD methodology. If coaching accuracy reaches 98% or extra in a number of iterations, in situ studying ends early. This loop is repeated 64 occasions, cumulatively querying 64 constraints, leading to a ultimate coaching dataset of 128 samples.

We efficiently demonstrated the in-memory energetic studying strategy of this job utilizing the ESCIM system. We used a digital laptop to arrange a three-dimensional (3D) tabletop simulator with a robotic and management DBAL loop, as proven by the orange and light-weight inexperienced elements of Fig. 4a (‘Experiment system setup’ part in Methods). Supplementary Fig. 9 reveals the pseudocode for the robotic’s ability studying job utilizing the in-memory DBAL framework. Our energetic studying methodology was extensively evaluated utilizing the simulator. The ESCIM system, related to the digital laptop, learn and modulated memristor arrays’ conductance throughout BDNN prediction and in situ studying, as proven by the grey elements in Fig. 4a. Supplementary Be aware 7 supplies further technical particulars on the robotic’s ability studying course of. Determine 4b depicts the memristor BDNN’s coaching classification accuracy evolution throughout 4 completely different coaching dataset sizes, indicating excessive accuracy throughout all networks. Notably, with 64 coaching samples, in situ studying stops early as a result of smaller information dimension’s decreased complexity and noise. The memristor conductance state distribution of the preliminary and finish of the energetic studying loop is proven in Fig. 4c. We additionally measured the passive studying methodology for comparability, which randomly selects samples for querying as an alternative of on the premise of prediction uncertainty. Determine 4d reveals the classification accuracy of energetic and passive studying methodology with unseen testing information. Rising coaching information dimension usually enhances the mannequin’s generalization and check accuracy. It may be seen that preliminary community classification accuracies of each strategies are comparable. Nonetheless, as question samples enhance, energetic studying outperforms passive studying, enhancing by about 13%. We additionally analyze the impression of cycle-to-cycle variability on community’s efficiency over time (Supplementary Be aware 8). The community maintains secure efficiency over time, with accuracy ranges much like these put up in situ studying (Supplementary Fig. 10). The rationale for the soundness could also be that the BDNN can inherently tolerate sure weights’ variations attributable to cycle-to-cycle variability. Moreover, we in contrast the educational efficiency of energetic and passive studying on the pouring ability job (Fig. 4e), with outcomes exhibiting that energetic studying outperforms passive studying with the identical variety of question samples.

We visualized the method of the robotic pouring the beads from the cup into the bowl utilizing energetic studying, as proven in Fig. 4f and Supplementary Film 1. We additionally visualized the ultimate tipping angle of the cup on the finish of the execution of the pouring motion by the robotic. Determine 4g reveals a dataset of pouring management parameters for a single bowl and cup pair by exhibiting the ultimate place of the crimson cup. We discover that the memristor BDNN learns that both the cup has a bigger pitch and is positioned instantly above the bowl or the cup has a smaller pitch and is positioned barely to the fitting of the bowl. This implies that the memristor BDNN is capturing intuitively related data for a profitable pour. These outcomes present that the proposed strategies may notice environment friendly in-memory DBAL.

Furthermore, we evaluated the power consumption and latency of stochastic CIM computing system on this studying job (Supplementary Fig. 11 and Prolonged Information Desk 1) after which in contrast it with a conventional CMOS-based graphics processing unit computing platform (Supplementary Be aware 9). The stochastic CIM computing system achieved a outstanding 44% enhance in velocity and conserved 153 occasions extra power. This velocity could possibly be additional improved by using high-parallel modulation strategies, and the power value could possibly be additional minimized by refining the ADC design (Prolonged Information Fig. 9). Resulting from in-memory VMM and in situ sampling facilitated by the intrinsic bodily randomness of studying and conductance modulation, memristor crossbars are able to enabling each in situ studying and prediction, thus overcoming von Neumann bottleneck challenges.